Editor's Note: This is the third in a six-part series on centrifugal pump efficiency. For other articles in this series, click here.
Hydraulic Efficiency
The shape and spacing of the impeller vanes have an effect on overall pump efficiency. Although the ideal impeller would have an infinite number of vanes, the real world limits us to five to seven for clear water pumps and even fewer for pumps that handle larger solids.
Also, flow would always be exactly parallel to the vane surfaces, but that does not happen either. Oddly enough, if the designer follows some well-documented rules, impeller vane efficiency losses remain relatively flat (about 2.5 percent) across a specific speed (Ns) range of 500 to 7,000.
Disk friction, which is caused by contact between the fluid and the impeller shrouds and hub surfaces, can reduce impeller efficiency another 4 to 15 percent at specific speeds below 2,000 but decreases to 2 percent or less at a specific speed of 3,000 and higher. Depending on its design, the impeller can reduce overall pump efficiency by as little as 4.5 percent or as much as 17.5 percent.
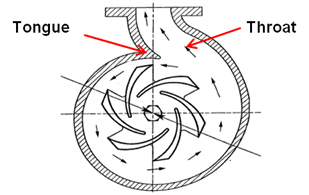
The volute also plays an important role in pump efficiency. At specific speeds below 2,000, friction losses range from 1 to 2.5 percent, but losses can approach 10 percent at a specific speed of 5,000 and higher. Typically, volute design begins with the throat (see Figure 1).
Its cross sectional area will determine the flow velocity out of the volute. Flow through the throat and other portions of the casing follows the law of constant angular momentum. Therefore, the designer will try to avoid abrupt changes in its nearly circular geometry while gradually increasing its volume.
Figure 1. Pump volute
Another critical area of the volute is the clearance between the outer circumference of the impeller and that of the volute tongue or cutwater. As this distance becomes larger, an increasing volume of liquid escapes entry into the volute throat and recirculates back into the volute case. The smallest distance that does not give rise to pressure pulsations during vane passing will produce the best efficiency. As a general rule, 5 to 10 percent of the impeller radius tends to be a safe value. The next section explains this in more detail, comparing the efficiencies that result from trimming an impeller versus changing its rotational speed.
Volumetric Efficiency
Whether the volumetric efficiency of a centrifugal pump is a function of the volute or the impeller is debatable (it is probably both), but I will include its effect here. Volumetric efficiency represents the power lost due to flow leakage through the wearing rings, the vane front clearances of semi-open impellers and the balancing holes in the rear shroud.
Leakage usually increases with a decrease in specific speed, flow or a combination of the two. For example, at a specific speed of 500 and a flow of 100 gallons per minute, leakage can account for as much as 7 percent of the total power consumed. At 2,000 gallons per minute, it is reduced to about 2 percent. At higher specific speeds and flows, volumetric losses can be as low as 1 percent.
Mechanical Efficiency
The final piece of the pump efficiency puzzle is that of mechanical losses, although some of these losses are not always included in published efficiency curves. In the case of a frame-mounted pump, these losses are caused by the shaft bearings and the mechanical seal or packing. For close-coupled pumps, bearing losses are figured into the motor efficiency. Again the rule of thumb follows that of volumetric efficiency, and losses increase as flow and/or specific speed decrease.
If the same values of specific speed and flow as in the volumetric example above are used, we could expect losses of 5 percent and 1 percent for a frame-mounted pump. At higher specific speeds and flows, mechanical losses can drop below 1 percent.
 Figure 2. Simplified total efficiency
Figure 2. Simplified total efficiency
Combined Efficiency
When looking at the overall efficiency of a pump in operation, the efficiency of the driver must be included, and in many instances, that driver will be an electric motor. When the Energy Independence and Security Act of 2007 went into effect in December 2010, it raised the bar on motor efficiency. Today, all new motors must meet premium efficiency standards. Obviously, a higher efficiency motor will increase the overall efficiency of a pumping system, but by how much? How do we calculate the combined efficiency of pumps and motors?
When I ask this question in my hydraulics classes, the common sense response is that it is the average of the two efficiencies. After all, the efficiency of two or more pumps, operating in parallel, is equal to the average of their individual efficiencies at their operating points.
However, when machines operate in series, their combined efficiency is different. Just as the total efficiency of a centrifugal pump is the product of several different internal efficiencies, so is the total efficiency of a pump and its driver.
The total efficiency of an electric motor and a centrifugal pump (wire to liquid or wire to water efficiency) is the product of the individual efficiencies. Sometimes, this is hard to visualize due to the units of measure used to compute the two efficiencies. Figure 2 simplifies this by using a single unit of measure that can be used to describe the operation of any machine. That unit is a “bag” of energy.
In this example, the motor consumes 10 bags and produces 9 bags, so its efficiency is 90 percent. The pump consumes the 9 bags provided by the motor and produces 7, so its efficiency is 78 percent. Therefore, for every 10 bags of energy consumed by the motor, 7 bags are produced by the pump, and the total efficiency of the system is 70 percent (7 bags / 10 bags).
This confirms that the product of the two individual efficiencies is the total efficiency of the system (90 percent x 78 percent = 70 percent). If this system is controlled by a VFD with an efficiency of 97 percent, the total efficiency will be reduced to 68 percent (at full speed, 60 Hz). This lower efficiency is the product of the three individual efficiencies.
Next month, the column will cover the efficiency savings that can be achieved by reducing the speed rather than trimming an impeller.
Pumps & Systems, April 2012