Editor's Note: This is the first article in a two-part series on Daniel Bernoulli. The series is part of a larger ongoing series on the history of pumps.
Have you ever noticed that the pressure produced by a centrifugal pump is usually lower when measured at the volute discharge than when measured downstream of the concentric increaser that connects the pump to the piping system? Does pressure have something to do with pipe diameter?
The work of Daniel Bernoulli explains a lot about the flow of fluids, and his work was one of the earliest examples of conservation of energy. This two part series will briefly describe the life and work of Daniel Bernoulli and provide examples of how we in the pump industry still benefit from his work in fluid dynamics.
Bernoulli’s Life & Work
Daniel Bernoulli was born in Groningen, Netherlands, in 1700 and came from a family of scientists and mathematicians. His father, John, occupied the chair of mathematics at Groningen and is remembered for his work in calculus and other mathematical areas. Unfortunately, he also had a bad side, and after losing a mathematical contest to Daniel, he kicked him out of the house. They never revived their relationship.
It did not stop there. John Bernoulli also published a book that plagiarized Daniel’s famous book, Hydrodynamica, and even changed the dates to make Daniel’s discoveries look like his own. John Bernoulli was not an ideal father. Fortunately, that did not deter his son.
As a student, Bernoulli studied mathematics, physics and medicine. All three directed him toward the flow of fluids. At 25, he and his contemporary, Leonhard Euler (another fluid flow student), studied the relationship of velocity and pressure during the flow of blood.
They punctured pipes, inserted thin glass tubes and observed that the height to which the fluid rose was proportional to the internal pressure of the pipe. Within a couple of years, physicians throughout Europe were measuring blood pressure by sticking sharp pointed glass tubes directly into their patient’s arteries. It was not until the 1890s that an Italian physician developed the much less painful method that is still used today.
Bernoulli’s work on fluids culminated with the publication of his book, Hydrodynamica in 1738. Figure 1 is a diagram from this book that he used to show how pressure could be measured in a flowing conduit. This technique was used almost exclusively for more than 100 years.
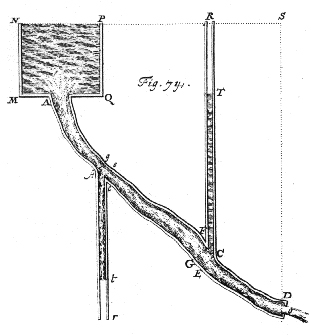
Figure 1. Illustration of how pressure can be measured in a flowing conduit
In 1849, Eugene Bourdon (France) patented the bourdon tube pressure gauge that revolutionized pressure measurement and is currently the primary technique used.In 1852, Edward Ashcroft (U.S.) purchased his patent and became one of the largest manufacturers of pressure gauges in the world.
Bernoulli’s studies were not limited to fluids. During the same period, he and Euler also developed the Euler-Bernoulli Beam Theory, which became a cornerstone of structural and mechanical engineering. However, after the publication of this book, his interests focused more on medicine than mathematics and physics.
The Bernoulli Principle
The Bernoulli principle is a simple and useful outcome of Bernoulli’s work in fluid dynamics. In its simple form, it states that the pressure of a fluid decreases as it velocity increases and vice versa. It is the consequence of the conservation of energy and explains many things that occur in nature. A fluid that is flowing steadily possesses three types of energy:
• Kinetic energy due to velocity
• Potential energy due to pressure
• Gravitational potential energy due to elevation
If no energy is added or removed from the system, the sum of these three remains constant.
Figure 2 is a simple illustration of the Bernoulli Principle. In this example, fluid flows from left to right at a constant rate of 50 gallons per minute (gpm). The left and right hand portions of the pipe are the same diameter while the middle section is constricted. The pressure gauges mounted on top of the pipe read 50 psi in the larger diameters and 48 psi in the constricted area.
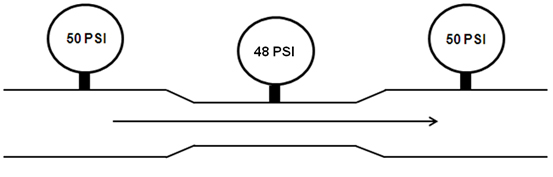
Figure 2. Simple illustration of the Bernoulli Principle.
After a little thought, it becomes obvious that, if the fluid is to maintain its original rate of flow as it enters a constricted area, its velocity must increase. We see this in nature when a slowly flowing river becomes a raging torrent as it passes through a narrow gorge. It may not be as obvious why a corresponding decrease in pressure occurs. Let’s get Isaac Newton’s input on this.
Newton’s first law of motion states that a fluid, in and of itself, will never undergo a spontaneous increase or decrease in velocity. His second law supports this by stating that some force is required to accelerate the fluid to a higher velocity. However, in our example, what is the source of that force?
The decrease in pressure in the constricted portion of the pipe allows the higher pressure in the un-constricted area to accelerate the fluid to a higher velocity. As it exits the constricted area the process is reversed and velocity decreases due to an increase in pressure (deceleration).
If our example used extremely accurate gauges, the gauge on the right would probably read a little less than 50 psi. This would be due to a small reduction in energy, in the form of heat, due to friction within the constricted portion of the pipe.
Bernoulli’s Principle can be derived directly from Newton’s second law and from the law of conservation of energy. Next month, I will review the forms of Bernoulli’s equation and show how it can be used to generate the hydraulic and energy grade lines that are used to predict pressure gradients in piping designs and open trench flow.
Mark Mitchell developed an excellent, interactive animation that allows visitors to change pipe diameters and witness the resulting changes in pressure and velocity. It is available at http://mitchellscience.com/bernoulli_principle_animation. This site also shows both derivations of Bernoulli’s equation and links to many other interesting sites.

