I received interesting (and challenging) feedback from our readers on “Resonant Frequencies, Part 1” from the July issue of Pumps & Systems. Relating mechanical resonance to the electromagnetic effects in biological systems—including humans, bacteria and pathogens—is becoming a new technology similar to what initially might seem like a far removed field. However, many similarities can be discovered upon closer analysis.
Comments from a Reader
Thanks for your interesting July article, “Resonant Frequencies,” which discussed vertical pump shaft, human and soft tissue resonant frequencies. In regard to the other factors that might be considered before using a simplified formula analysis (for example, Equation 1), the following might be considered:
A significant difference in the surrounding temperature (from ambient) could affect the elasticity modulus, E.
Closely spaced shaft sections (between stages) may affect the end condition, βn, of an adjacent, long length of shafting (such as the use of a clamped-end condition instead of simply supported at that location). Hanging weight and hydraulic axial thrust, F (added tension), acting on the end of a length of vertical pump shafting can affect the frequencies.
ωn2 = βn4 x EI / (m/L) [Equation 1]
The following is a modification of Equation 1 to approximately account for the effect of added axial shaft tension:
ωn2 = βn4 x E I / (m/L), can be rewritten as
ωn2 = (βn2 x E I) x βn2 / (m/L)
Now add additional axial loading, “F,” to the axial force (βn2 x E I), and the revised Equation 1 becomes:
ωn2 = (βn2 x E I + F) x βn2 / (m/L)
This can then be written as:
ωn2 = ωn(0)4 + βn2 x F / (m/L)
Where:
ωn(o) is the frequency without axial loading from the original Equation 1.
Under “Examples” in the July article, a possible problematic shaft diameter between 1.8 and 2.4 inches is mentioned. However, the natural frequency for the existing 1.8 diameter shaft in Case B is only about 8 percent from the operating speed. I probably would want to see a larger margin to avoid potential lateral shaft vibration. Since the calculated natural frequencies for both the 1.44 and 1.8 diameter shaft sections are below the operating rpm, the pump will pass through these resonant speeds for a short duration while starting up or shutting down. Of course, variable speed applications could add another dimension to consider.
In the article, the natural frequency for humans and soft tissue seems to be based on simply supported boundaries. I probably would have also looked at clamped-free for a standing human and free-free for soft tissue. The Smithsonian/NASA Astrophysics Data System reports vertical (standing) whole-body human resonant frequency between 5 to 10 hertz. http://adsabs.harvard.edu/abs/2001SPIE.4317..469B.
From a different article, “In 1992, Bruce Taino of Taino Technology, an independent division of Eastern State University in Cheny, Wash., built the first frequency monitor in the world. Taino has determined that the average frequency of a healthy human body during the daytime is 62 to 68 hertz.” Perhaps this frequency is when lying down? http://cellphonesafety.wordpress.com/2006/09/17/the-frequency-of-the-human-bodyand-your-coffee/.
Another interesting article addressing muscle damping can be read at http://jap.physiology.org/content/93/3/1093.full.
Lee Ruiz
Oceanside, Calif.
Follow-up
I applied Ruiz’s input to correct some of my numbers that were originally presented in July. I also did more research and found a good article—“Morphological Transformations of Human Cancer Cells and Microtubules Caused by Frequency Specific Pulsed Electric Fields Broadcast by an Enclosed Gas Plasma Antenna,” Proceedings of 7th International Workshop on Biological Effects of EMF, October 2012 (Malta), ISBN 978-99957-0-361-5—published by Anthony Holland, James Bare and their coauthors. The article is online at www.pump-magazine.com/pump_maga zine/editorial/editorial.htm. Click the “Anthony Holland ASM 2012” link.
The basis of Holland’s article relates the electromagnetic field’s effects on mechanical resonance because it helps generate and excite biological cells of different pathogens with the goal of vibrating them (mechanically, or at least assistive mechanically) to destruction, ridding the body of the harmful pathogens. The authors had a good correlation between their theory and their tests. The key items within the formulas (from a mechanical engineering view) are the density of the pathogen and its modulus of elasticity (E). The end conditions also changed the resultant naturals.
The value that the authors use in their paper for biological pathogens is 2,900 psi versus the 500,000 psi that I used in my July article. The formula from my article predicts a 73-kilohertz resonance for the pathogen that Holland’s team studied. Although this figure is somewhat off the calculation in their paper (100 kilohertz is shown in Table 5), 73 kilohertz is at least a reasonable correlation. Perhaps incorporating a correction of the axial force stiffening effect into Holland’s calculation could explain the discrepancy between the 100 kilohertz measured and the calculated 73 kilohertz. In Table 1, the “beta x L” factor of 4.73 (both ends clamped) was also assumed by Holland’s team. The original dimensions of the pathogens used by the authors were in metric units in their paper and converted to the U.S. system in Table 1.
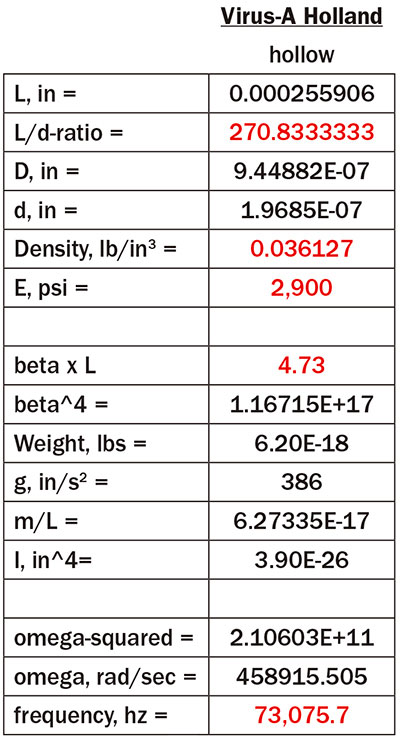 Table 1. Resonant frequency of Virus A,
U.S. units
Table 1. Resonant frequency of Virus A,
U.S. unitsHolland’s team also showed that, similar to what Ruiz pointed out, temperature has an effect. Young’s modulus must triple to produce the same natural frequency when the temperature drops from 37 C to 20 C. The authors also determined the pathogens’ density to be equal to the density of water, which seems to be reasonable since our bodies are made mostly of water.
However, the value for the modulus of elasticity that I used in my article was 500,000 psi, which is also what I used to calculate the natural resonant frequency of a standing human, which is where the 72.9 kilohertz originated. Table 2 shows a corrected calculation, using 2,900 psi for the modulus, as recommended by Holland’s paper. The resultant correction shows a 5.6 hertz (not my original 73 kilohertz) resonance for a standing human, which now correlates better with Ruiz’s referenced 5 to 10 hertz value from the Smithsonian/NASA Astrophysics Data Systems report.
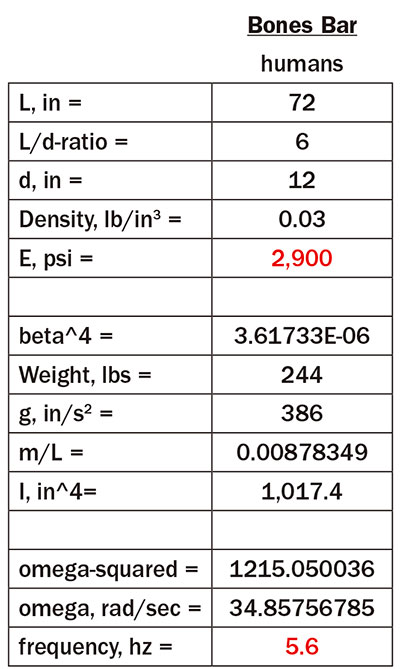 Table 2. Resonant frequency of bones
Table 2. Resonant frequency of bonesInterestingly, my original use of a higher module of elasticity was based on assuming that the body’s elasticity behaves similarly to the bones (which have a higher modulus of elasticity). Apparently, as a side observation, bones do not contribute significantly to the stiffness factor of natural frequency calculations (see Table 2).
One point that remains unclear is the basis of the Young’s module of elasticity that was used in Holland’s paper. It is also not clear why the assumed end conditions are clamped. Perhaps they were made simply so that the results correlated better with the testing they described and may require some clarification.
There are also some errors in the formulas (such as Equation 11, which appears to be missing the diameter, “D”). Given the obvious difficulties of knowing the exact mechanical characteristics of the complex strictures of human bodies or even the strictures of pathogens (viruses and bacteria), the results cannot be expected to have absolute agreement between theory and tests.
A working group (also described in the same link as the paper) has been formed to relate mechanical and biological structural resonance effects. If any readers are interested, they are welcome to join.
The immediate interest is to see if electromagnetics can induce resonance in mold spores and prevent bread from molding. Many of the people in this group are mechanical engineers (familiar with mechanical resonance in industrial machinery, such as pumps), although some are electrical engineers. We could use experienced radio engineers to help answer some questions from the group.
A follow-up paper will be presented at the American Society of Mechanical Engineers Conference on nano technology in San Diego in November.

