First of Three Parts
This three part primer is a basic introduction to AC power for those in the pump industry who need a place to start. It will also provide several web references to access if you would like to further your understanding of this interesting and essential topic.
What is Electricity?
The dictionary defines electricity as "a fundamental property of matter caused by the presence of electrons and protons, and manifesting itself as attraction, repulsion, luminous & heating effects, and the like." Did that peak your interest?
I think that my definition is more meaningful: "An elegantly simple yet incomprehensible entity that moves at the speed of light yet can remain trapped in wires destined only to bounce back and forth; weightless but still breaks the sound barrier as it plummets from the clouds; attractive yet repulsive; a taker of lives but also a restorer of life." This sounds a little more interesting, but I have to admit that it is still a bit vague.
Like many other properties in physics, electricity is difficult to define. It more easily lends itself to descriptions such as attraction and repulsion. It can fundamentally be described as a force just as gravity is force, or as a form of energy. It can be static or it can be moving. Since electricity is so difficult to define, it is probably best that we just try to describe it and its effects.
AC Versus DC: A Little History
"A chicken in every pot and an eagle in every pocket" was a slogan during the Great Depression. Had Thomas Edison won the battle over power distribution, we could have added "and a power plant on every corner." Edison was a great proponent of DC power and fought the use of AC bitterly. He invented the incandescent lamp in 1879 and began to develop a power generating and distribution system to promote it. He opened his first power plant in New York City in 1882 and added several others during the next few years.
His plan was to build a power grid with generating stations about four miles apart. Although Edison's efforts were a limited financial success, it was soon recognized that DC transmission systems suffered heavy power losses over any significant distance.
Edison's principal opponent at the time was George Westinghouse. He and his partner, a Serbian-American engineer named Nikola Tesla, made long distance AC transmission practical. Tesla invented the transformer and induction motor, made major improvements in the AC generator and was awarded more than 100 patents.
In the late 1880s, LL Nunn, a mine owner from Telluride, Colo., came to Westinghouse with a proposal to build a steam powered AC power plant for his mine. Westinghouse accepted the offer, and when it went online in 1891 it was the first AC power plant in the world. It eventually became part of Nunn's Telluride Power Company, which is now part of Utah Power and Light.
In 1893, Westinghouse won a contract to construct a commercial AC hydroelectric plant at Niagara Falls. This plant convincingly demonstrated the flexibility of AC power and relegated DC to a secondary role. If you want to learn more about the bitter battle between Edison and Westinghouse, go to http://en.wikipedia.org/wiki/War_of_Currents.
Common Electrical Terms (AC and DC)
Volt: A unit of potential difference. It is the difference in electromotive force (or charge) between two points. A reasonable analogy for those familiar with pumping applications is pressure. Voltage in an electrical circuit is similar to pressure in a pipeline.
Ampere (Amp): A unit of current or the amount of the current in a circuit. When compared to water in a pipeline, Amps or current is similar to flow in gallons.
Ohm: A unit of resistance that impedes the flow of current in a circuit. Again, when compared to our pipeline, it is analogous to friction.
Watt: In the English system, the Watt is a unit of power and, in its simplest form, is the product of volts times amps. It is similar to the energy possessed by water in a pipeline, which is the product of flow and pressure.
AC/DC Pros and Cons
Why was DC power so attractive to Edison and its other followers? DC power is extremely simple when compared to AC. Once a DC voltage is switched on, its intensity remains constant unless something in the system changes. It also follows Ohm's law. Just about everything you need to know about a DC circuit is described by: I = E/R (or E = IR) where E is voltage, I is current and R is the resistance. If simplicity is not enough, it can even be stored by a battery.
One of the major advantages of AC power is that its voltage can be changed easily by the transformer, a device that operates on the principle of induction and takes advantage of the relationship between the volt and the ampere. That relationship states that power in watts is equal to volts times amps where volts and amps can be any quantity. One kilowatt (kW) can be 100 volts at 10 amps or it can be 1,000 volts at 1 amp.
When transmitting power over long distances, the combination of higher voltage and lower amperage results in lower transmission losses because the energy expended (as heat) in maintaining current flow increases as the square of current intensity. In other words, if you reduce voltage by one half while leaving power constant, losses due to heat will increase by four.
DC voltage, on the other hand, is difficult to change and typically must be generated at the same voltage at which it will be consumed. Therefore, DC current intensity will always be disproportionately high and energy losses will follow the rule I just stated.
Another advantage is that AC current can be generated as a single wave form (phase) or in multiple waves (phases). We will talk more about this advantage next month. Also, its frequency (cycles per second or hertz) can be varied easily during generation or afterward. Finally, it is easy to convert AC to DC when DC is needed but more expensive to convert DC to AC.
On the downside, AC power is far more complex than DC. Fortunately, this is not a major factor as all of its complexities have been studied and understood by those before us. If we follow the known rules, we can use all of its benefits and avoid any pitfalls. We will take a look at this more complex power curve.
The AC Power Curve
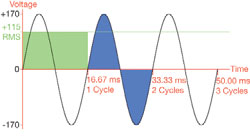
The single phase, 120 V sine wave shown in Figure 1 has several important characteristics. As it progresses through one full cycle (one 360 deg rotation of a generator), it begins at 0 V, then peaks at 170 V a quarter of the way through the cycle. It returns to zero at the halfway point and then reaches negative 170 V at 270 deg. At the end of the cycle it returns to 0 V. In the United States, this occurs 60 times each second, so one full cycle takes about 16.67 milliseconds. A full cycle is also known as a Hertz (Hz). Three complete cycles are shown in the illustration.
 |
| Figure 1 |
You are probably wondering why we call this a 120 V sine wave if the actual peak is at 170 V. Could 120 V be the average? If you were to average all of the voltage values, the result would be approximately 108 V, so that must not be the answer. Why then is the value, as measured by a Volt/Ohm Meter (VOM), equal to 120 V? It has to do with something called effective voltage. It turns out that the area of the green rectangle, whose upper border is at 120 V, is equal to the sum of the actual areas under the upper and lower curves of a single AC cycle (blue areas). This area is known as the effective voltage of the sine wave. We will take a closer look at effective voltage.
If you were to measure the heat produced by a DC current flowing through a resistance, you would find it is greater than that produced by an equivalent AC current because AC does not maintain a constant value throughout its cycle. If you did this in the lab, under controlled conditions, and found that a particular DC current generated a heat rise of 100 deg, its AC equivalent would produce a rise of only 70.7 deg or 70.7 percent of the DC value. Therefore, the effective value of AC is 70.7 percent of DC. 0.707 times the peak voltage of 170 in Figure 1 equals 120 V.
Also, the effective value of an AC voltage is equal to the square root of the average of the squares of the voltage values across the cycle(√v12+v22+ •••vn2/n). Thus, effective voltage is known as the root mean square, or RMS voltage. A simplified form of the RMS equation is vp/√2 where vp is the peak voltage. If the peak voltage were 1, the RMS calculation will also yield 0.707. It follows that the peak voltage will always be 1.414 that of the effective or RMS voltage. Remember that unless stated otherwise, all VOMs are calibrated to display RMS voltage.
Next month we will discuss the relationship between peak voltage and frequency and then move on to three phase power.
Pumps and Systems, June 2010

