A Simplified Method for Monitoring Pump Performance
Selecting the Optimum Field Test Method
Monitoring performance in the field has always been a challenge due to an absence of field-mounted instrumentation, the time required for testing, and imprecision from the cumulative uncertainty of all performance variables involved.
Last month I reviewed a practical, cost-effective, and environmentally-friendly pump performance assessment method to determine the pump’s health and whether repairs are economically justified. That simplified method, as researched by D. Budhram, M. Russek, and myself, advocates using only motor power and flow measurements to determine if a pump is healthy or worn.1
The purpose of this column is to refine some of that original research and introduce a new means of determining which field analysis method is best for your situation. Centrifugal pump users have several pump assessment methods to choose from. Each one has its own advantages and disadvantages. Here are the most common.
Single-Variable Method
- Head at shut-in conditions – Using this method, you run the pump dead headed and measure the pump’s differential pressure. This method requires a pump curve and the willingness to shut the pump in long enough to gather the data.
Two-Variable Methods
- Head vs. Flow – With this method, you can test the pump at any flow rate. You measure the output flow (QM) and compare it to the apparent flow (QA). The apparent flow is the test curve flow that corresponds to the field-measured differential pressure. This method requires a test curve from the manufacturer.
- Power vs. Flow – Using this method, you can also test the pump at any flow rate. With this method, you measure the output flow (QM) and compare it to the apparent flow (QA). The apparent flow is the test curve flow that corresponds to the field-measured horsepower. This method requires a test curve from the manufacturer.
- The two-variable methods assume that the apparent lost flow (QA-QM) is due to internal leakage and can be reestablished by renewing internal clearances.
Three-Variable Method
- Head, Flow, and Power – With this method, you can test the pump at any flow rate. This method doesn’t require a test curve. By measuring head, flow, and power you can determine the pump’s hydraulic efficiency directly.
(Note: I consider H, Q, and P to be primary (measured) quantities and hydraulic efficiency to be a secondary (calculated) quantity. This is because efficiency has the greatest percent error of all test stand results due to the fact that errors in all the primary testing quantities, i.e. H, Q, P1, P2, and S.G., “stack-up” during the calculation of η. For this reason, efficiency is not the best choice for trending pump condition under field conditions.)
A New Method
The original research recommended the Power vs. Flow method for pumps with low specific speeds (< 3000) to ensure the horsepower vs. flow slope is both positive and easy to resolve into reasonably small horsepower increments.
I now realize this was a rather vague guideline without a clear technical basis. A major goal of this column is to better quantify when head vs. flow method should be used, and when the power vs. flow method should be used.
I first began my analysis by approximating a general performance curve with a straight line (see Figure 1). The line has the general form H = Ho + mQ, where Ho is where the tangent line at the best efficiency point (BEP) intersects the abscissa and m is the slope of the tangent line. I assume the efficiency is constant over the flow range of interest, which is a good assumption at BEP. (Note: Ho should not be confused with the pump’s shut-in pressure.)
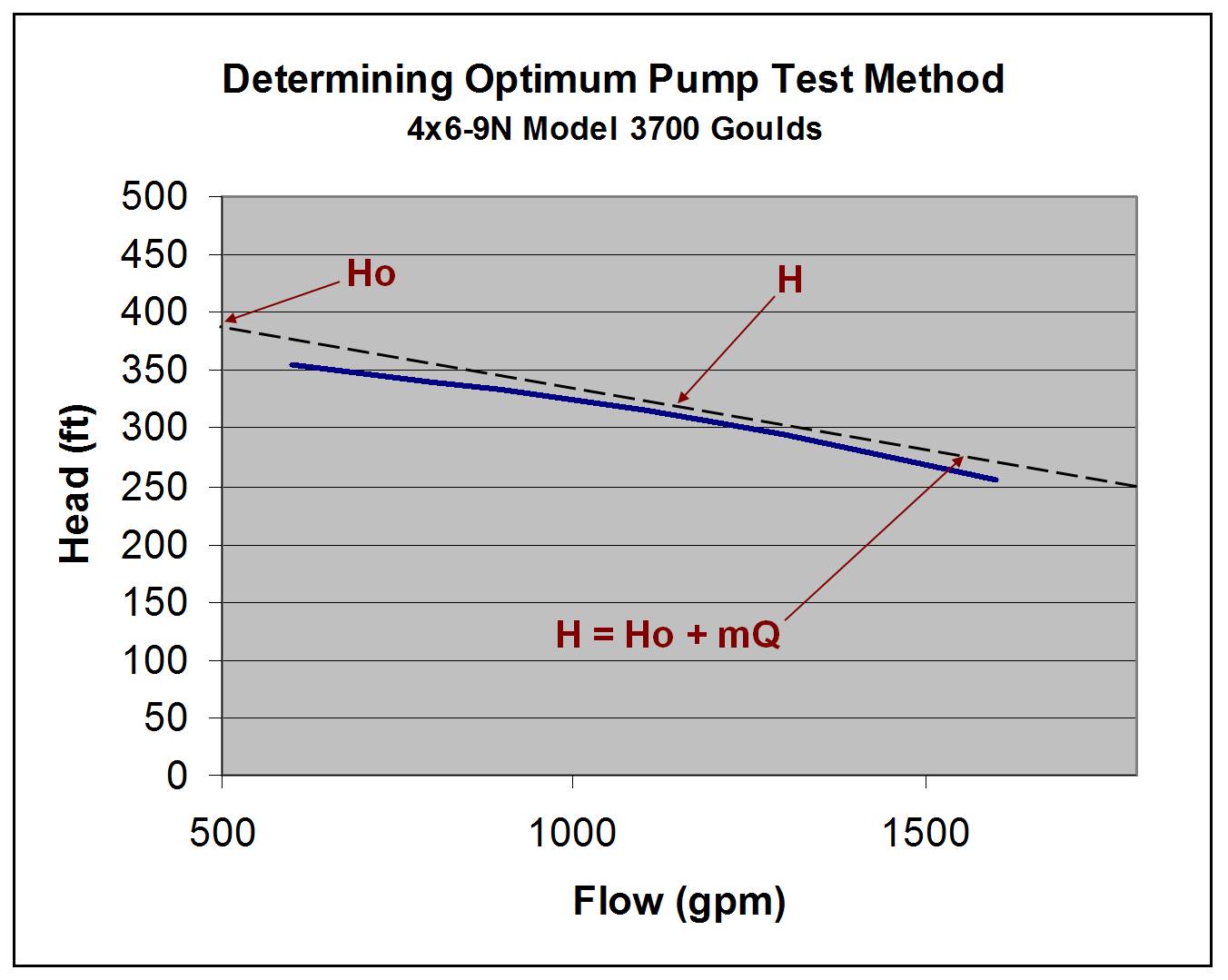
Figure 1. Typical pump curve with simplified performance line.
- Starting with this approximation, my aim was to determine whether pressure or power measurements would lead to higher uncertainty in apparent flow (QA). What good is an accurate measured flow (QM) if the QA is excessive? The desired result of a field assessment is to determine the ΔQ value, which is equal to QA-QM. The uncertainty in the flow discrepancy (ΔQ) is:
Uncertainty in the flow discrepancy = ((Uncertainty in QA)2 – Uncertainty in QM)2)0.5
To reduce the uncertainty in ΔQ to useful levels, we must ensure the uncertainty in both QA and QM are also at useful levels.
I will not include the derivation of what I call the flow error ratio (Ø) parameter here, but anyone interested can find it in the appendix. I will only present only the results here. The Ø parameter, which is the ratio of apparent flow error (ΔQH) expected when using the head vs. flow method to the apparent flow error (ΔQP) expected when using the power vs. flow method is given by the following equation:
Where ΔQH/ΔQP is the error ratio parameter, R is the ratio of percent error in head (%H) to the percent error in power (%P), and h is H/Ho. (Note: Here H is the head at BEP.)
Figure 2 is a plot of h versus Ø for various values of R. When the absolute value of the Ø parameter is >1, you should use the power vs. flow method. Conversely, when absolute value of the Ø parameter <1, you should use the head vs. flow method. Obviously, there are grey areas when the absolute value of the Ø parameter is slightly greater or less than when 1. In those cases, uses the method that is more convenient.
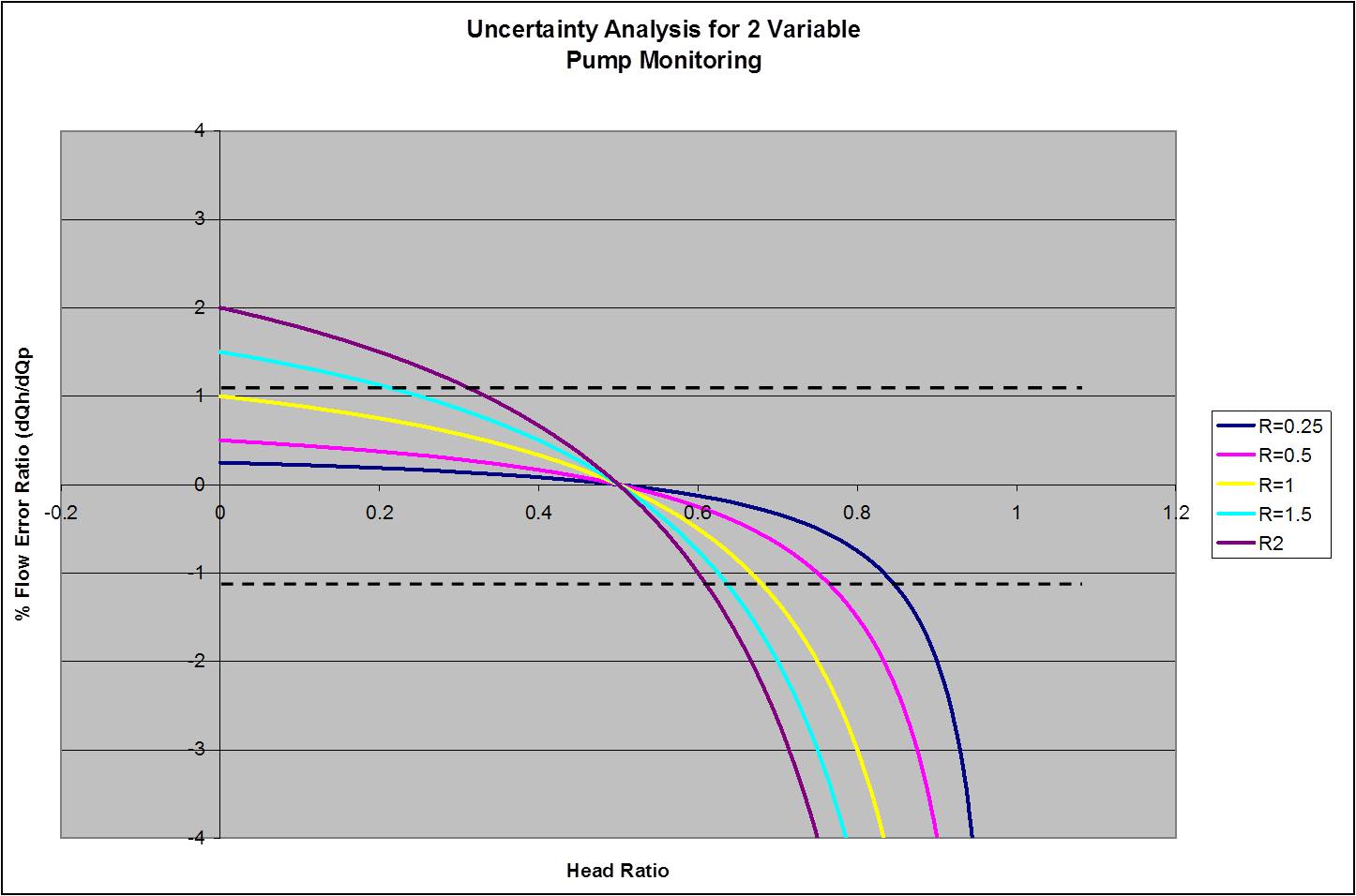
Figure 2. Plot of the FER parameter for various R values.
The Punch Line
For pump curves continuously sloping downward, which is the most common type of pump curve, the critical value for dQh/dQp is -1. Setting equation (1) to -1, we get:
pressure measurement is preferred Equation (4)
Example #1
Revisiting Figure 1, you will see Ho = 375 and H = 310. This means h = H/Ho = 0.827. If we know the percent error for our digital pressure gage is 1% and the percent error of our power meter is also 1%, we then know R = 1, so (R+1)/(2R+1) = 2/3. We can now conclude that power vs. flow is the preferred method, since 0.827 > 0.67.
Example #2
Use the curve in Figure 1, again h = H/Ho = 0.827. We know the percent error for your digital pressure gage is 1%, but we intend to use amps to estimate power; there our percent error of your power meter is about 5%. This means R = 0.2, so (R+1)/(2R+1) = 0.857. We can now conclude that head vs. flow is the preferred method since 0.827 < 0.857.
Example #3
H = 300, Ho = 400, and R = .5
h = 0.75
(R+1)/(2R+1) = 1.5/2
Therefore 0.75 = 0.75, so you can use either measurement method.
Example #4
H = 50, Ho = 100, and R = 1
h = 0.5
(R+1)/(2R+1) = 2/3
Therefore 0.5 < 0.67, so you should use pressure as a means of measurement.
You can see the flow error ration parameter, Ø is a powerful tool enabling pump users to select which two variable test method is best for their situation. Using the Ø parameter as a testing guideline will ensure your %QA error stays between 1% to 2%, for %H = %P = 1%. To further improve testing results, I offer the following testing tips:
1. Don’t depend on an analogue pressure gage unless it’s a test gage and has recently calibrated.
2. Do use digital pressure gages to ensure a 1% or less error.
3. Don’t use motor amps to estimate power.
4. Do use a power meter to ensure an accuracy of 1% or less.
5. Do use the most accurate flowmeter available. You can achieve a 2% resolution with a clamp-up transit time flowmeter.
6. Do ensure your instrumentation is calibrated before field testing.
7. Since your errors stack-up, try to keep all your errors < 2% or 1% if possible. For example, if you QM error is 5% and your QA error is 3%, you total error will be:
8. Do request test stand data for critical pumps so that you can easily monitor their condition.
Closing
This analysis underscores the fact that your results are only as good as your testing methods. If your error in ΔQ is greater than the acceptable flow loss due to internal wear, then you’re better off not even testing.
If you take the time and effort to obtain low uncertainty values through calibration and instrument selection and the use of the proper two-parameter method, you will greatly improve your chances of obtaining meaningful field test results. This will allow you to determine if your pump is healthy or not and when it’s time for refurbishment.
Works Cited
1 Budhram, D., Russek, M., and Perez, R., Hydrocarbon Processing, August 2002, pp. 47-52.
Pumps & Systems, November 2006
Appendix
Derivation of the Flow Error Ratio (Ø) Parameter Equation
6. P = k(Ho + mQ) x Q = k(H0Q + mQ2)
7. dP
(We assume efficiency is constant over the flow range of interest, i.e. near BEP)
10. dQH = %H x H
11. dQP = %P x HQ
13. dQH %H Ho + 2mQ %H [Ho %H [ Ho
where R is the ratio of head (H) percent error to power (P) percent error
16. dQH ΔQH 1
Further simplifiying we get:
17. Ø = dQH 2h−1

