Last of four parts
Last month, we studied the properties and effects of resistive, inductive and capacitive loads in an AC circuit. This month, we will take self induction a step further and apply it to that very simple machine that is at the heart of AC power—the transformer.
As I mentioned in Part One, (Pumps & Systems, June 2010)a unique quality of AC power is that its voltage can be changed easily and in either direction—up or down. This allows us to generate power at some voltage and step it up to a higher voltage for long distance transmission. This decreases losses due to heat and significantly reduces the wire size. Once it reaches its point of use, voltage can be reduced to a useable intensity. The key element in this process is the transformer, and the key to its operation is a phenomenon known as mutual induction.
Mutual Induction
If two coils of wire are placed near each other (see Figure 1), an alternating current flowing in one will create a magnetic field that induces a voltage and current in the one nearby, even though they are not in direct contact. This occurs because the lines of flux associated with the magnetic field extend well beyond the coil that created them. This property is called mutual inductance or mutual induction, and it is the basis of the transformer. The transformer gets its name from the process of transforming electrical energy into magnetic energy and then back to electrical energy. The coil that produces the magnetic field is called the primary (input) and the coil that intercepts that field is called the secondary (output).
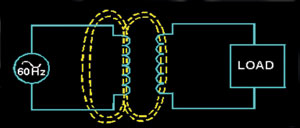
Figure 1
Although some transformers consist of coils separated by an air gap, most use insulated wire wound about a laminated iron core (see Figure 2). The iron core increases transformer efficiency by directing nearly all the flux produced by the primary through the secondary coil. The laminations reduce eddy current losses that would be much higher in a solid core design. Depending on the design and capacity, transformer efficiency can range from 20 to 99 percent. Larger ones—for example those designed for power distribution applications—operate at 98 percent or better. Another important property of the transformer is electrical isolation. Since the primary and secondary coils are not in contact, the power source is isolated from the point of use.
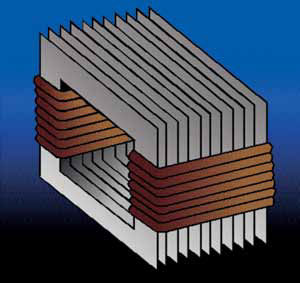
Figure 2
Voltage, Current and the Turns Ratio
According to Faraday's law, voltage produced in the secondary of a transformer depends on the voltage in the primary and the number of turns (loops) in the primary and secondary coils. This may sound a little complicated, but this relationship can be stated very simply with something called the turns to voltage ratio. The equation below—where V is voltage, N is the number of turns, p is the primary and s is the secondary—explains this relationship:
Vs = (Ns / Np) x Vp
Secondary voltage is directly proportional to the product of the turns ratio and primary voltage. If Ns is greater than Np, then the voltage in the secondary coil is greater than that of the primary coil, and the transformer is called a step-up transformer. If the opposite is true, we have a step-down transformer. For example, suppose a transformer has a primary with 1,000 turns and a secondary with 100 turns. Based on the equation above, the turns ratio is 1/10 or 0.1. If the voltage feeding the primary is 1,200 V then the secondary voltage will be 120V.
However, what about current? How do we calculate its change? The transformer is an intelligent machine because it automatically adjusts the current to keep power (in watts) constant. A slight modification of the original equation explains this relationship:
Is = (Np / Ns) x Ip
In the equation above, current (I) replaces voltage and the turns ratio is reversed. When fewer turns are in the secondary, a transformer steps down voltage, but it increases current and, therefore, keeps power constant. In the case of our step-down transformer example above, if the primary is fed by 1,200 V at 1 A, then the secondary would provide 120 V at 10 A. Both volt / amp combinations provide 1,200 W of power.
Winding Configurations
Transformers allow an extremely flexible secondary output and are not limited to a single secondary winding. Figure 3 shows an example of a typical power supply transformer. The primary is fed by 110 V and induces three individual secondary coils providing 5 V, 6.3 V and 700 V. The 700 V coil shows another feature of the transformer. A “tap” placed at the center of the coil provides two 350-V outputs in addition to its full voltage output. Multiple taps may also be placed within a single coil.
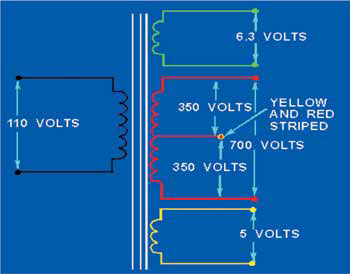
Figure 3
Three Phase Transformers
Transformers used in three-phase applications can consist of three, single-phase transformers or a single one wound in a manner that accommodates all three phases. The primary and secondary windings of the three-phase transformer are configured in two basic patterns—Delta and Wye. The primary and secondary can be any combination of the two (such as Wye/Delta, Delta/Wye, Delta/Delta and Wye/Wye). This article will examine the Delta and Wye secondary characteristics only. Additional resources are provided at the end of the article if you are interested in pursuing the effect of a particular primary on a secondary.
Figure 4 is the schematic of a Delta secondary that produces three individual phase voltages of 120 V. The Delta gets its name from the Greek letter that has a similar appearance. You might think that such a configuration would short circuit since they are connected in series. However, note the angle associated with each phase starting at the top and proceeding counter clockwise. If you refer to the three-phase power curve in Figure 3 of Part Two (Pumps & Systems, July 2010), you will see that the voltages cancel one another and no current flows through the circuit. If, however, a load is connected across any two of the three “lines,” a current will flow and the line–to-line voltage will be the sum of the phase voltages, which equals 240 V.
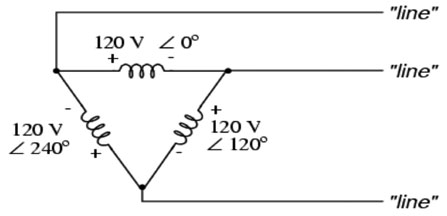
Figure 4
Figure 5 is the schematic of a WYE secondary that also produces three individual phase voltages of 120 V. It gets its name from its resemblance to the letter Y and is sometimes called a “star.” At the junction of the three phases, a separate connection, known as a “neutral” is usually supplied. A load connected between the “neutral” and any of the three “lines” will see a voltage of 120 V. When a load is connected across any two of the three “lines,” the voltage will not be the sum of the two phases. Instead, it will be approximately 208 V. The reason this occurs is due to the phase angle and the way the coils are connected. Although we will not show one here, a phasor diagram would illustrate that the voltage vector created by any two WYE phases produces a voltage that is only 1.732 that of the phase voltage. If you are interested in viewing WYE and Delta phasors, check out “The Changing Voltage Puzzler” on my website.

Figure 5
Based on the line-to-line voltage, it would appear that the WYE transformer is less efficient than the Delta. However, an interesting event occurs within the Delta configuration. A phasor diagram would show that the line-to-line current is only 1.732 of the phase current. Therefore, the relationship below will hold true for any circuit regardless of whether it is Delta and WYE connected.
Power (watts) = volts x amps x 1.732 x power factor
I hope that this brief introduction to AC power has been useful. There is a lot more involved, so below are several websites that you can visit for more information. In the future, I plan to write a similar series on AC motors.
Resources
All About Circuits: http://www.allaboutcircuits.com/vol_2/index.html
Integrated Publishing – EE Training Series: http://www.tpub.com/content/neets/
Electronics – Tutorials: http://www.electronics-tutorials.ws/index.html
Siemens: http://www3.sea.siemens.com/step/templates/lesson.mason?bep:2:1:1
Electrician's Toolbox: http://www.elec-toolbox.com/
RLC Circuits – Java Applet: http://www.walter-fendt.de/ph14e/accircuit.htm
Pumps & Systems, September 2010

