Editor's Note: This is the third article the year-long series, Understanding NPSH.
Effect of Gas on NPSH
Effect of Dissolved Gas on Vapor Pressure
Determining the vapor pressure of light hydrocarbons is fairly easy. They are usually at their vapor pressure ("bubble point") in the suction vessel. In such a case, the vapor pressure is equal to the vessel pressure. How about cool water? That's easy. A quick reference to the steam tables reveals its vapor pressure, right? Wrong! Steam tables give the vapor pressure of only pure deaerated water. Water has almost always been exposed to air, and cool water has a strong affinity for air. Water will absorb a significant quantity of air, and this air will flash out of solution as the pressure is reduced (such as in the eye of an impeller). Even water pumped from below ground contains a significant amount of air.Therefore, most water has an effective vapor pressure higher than pure water. The dissolved air increases the vapor pressure of the "solution." The air will flash out of solution at a pressure higher than the vapor pressure of pure water. Consequently, we do not have as much NPSH as we calculate using the vapor pressure from the steam tables. How can we compensate for this higher vapor pressure of cool water? Chan (1) has demonstrated that, for water that has been saturated with air in an atmospheric tank the effective vapor pressure can be approximated as the average of atmospheric pressure and the vapor pressure of air‑free water to calculate the NPSH available to a centrifugal pump.
Heavier hydrocarbons (vapor pressures below atmospheric pressure) have the same problem as water. They are usually stored in atmospheric tanks, and they absorb more air than water does (3). Kerosene is a good example of a heavier hydrocarbon that really soaks up air. Dissolved air has caused problems with pumps handling heavier hydrocarbons (3).
Other Sources of Gas (Entrained Gas)
Gas can come from sources other than cavitation of the liquid itself, or from dissolved gases. One source can be the suction vessel. If the submergence of the tank outlet to the pump is insufficient to prevent the formation of a vortex, pockets of gas will enter the suction pipe from the tank, eventually flowing into the pump. A vortex breaker in the tank can reduce the tendency of the liquid to form a vortex.
If liquid feeds into the suction vessel above the liquid level, gas bubbles will be carried down into the liquid, and may flow into the suction line. Therefore, the main feed line, and the minimum‑flow (by‑pass) line from the pump should feed into the vessel below the minimum liquid level.
Another source of gas can be the suction line itself. If any portion of the line is under a vacuum, air will leak into the line through gaskets and fittings that are not absolutely tight.
A valve in a suction line, under a vacuum, can leak air into the line though the stem packing.
The pump itself is also another source of gas. If the stuffing box, or seal chamber, is under a vacuum at any time while starting or running, air can leak through the packing or mechanical seal.
Design Systems to Exclude Gas
Although a few pumps, such as the minimum‑clearance reciprocating and the two‑screw rotary, have been adapted to handle some quantities of gas (they are really combination pump‑compressor), most pumps are not suitably equipped to handle free gas.
Although, as will be discussed in a future article, a small quantity of gas can reduce noise and damage in a centrifugal pump; any significant quantity of gas (more than about 2 percent) will have a detrimental effect on pump performance. For a high‑pressure reciprocating pump, any amount of free gas can seriously damage the pump. Operators of pressurized‑water reactor nuclear systems can attest to the latter.
For these reasons, it is considered good practice to design a system to separate all free gas from the liquid flowing into a pump. This requires careful design of the suction vessel.
Illustration of NPSH
Illustration of NPSH
Figure 1 may help clarify your understanding of NPSH. If the lower end of a closed vertical tower is submerged in an open tank of air‑free water at 80-deg, and atmospheric pressure is 14.7-psia (sea level), the column of water will rise in the tower when a vacuum is applied to the top of the tower. Atmospheric pressure actually pushes the water up into the tower.
Figure 1. Illustration of NPSH
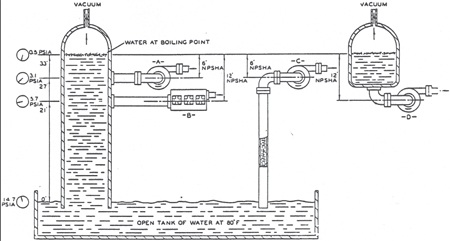
As the pressure in the top of the tower is further reduced, the water will rise further, until it is 33-ft above the level in the tank. The water will reach this level when the pressure above the water has dropped to 0.5-psia (about 29-in of mercury vacuum). Any attempt to further reduce the pressure and "lift" the water higher will fail. The water column will "break." Actually, the water will boil at the upper surface, pushing water vapor into the cavity above the water and preventing the pressure from dropping below 0.5-psia. Therefore, the vapor pressure of water at 80-deg is 0.5-psia.
We will hold the column of water at these conditions, and mount a pump at the side of the tower, taking suction from the tower. If this pump requires 6-ft of NPSH, how high on the side of the tower can the pump be mounted for satisfactory operation? The answer, 6-ft below the surface of the boiling liquid (assuming no friction loss or acceleration head) or 27-ft above the tank surface (position A). If a pump requires 12-ft of NPSH, it should be mounted no higher than position B (12-ft below the surface of the boiling water).
A pump operating at position C, with a separate suction line (again assuming no losses), will be subjected to the same suction conditions as the pump in position A. The water above the pump in position A actually has no effect on the pump. Similarly, a pump operating at position D will be subjected to the same suction conditions as the one in position B (again assuming no losses).
Any system can be analyzed in a similar fashion if the actual vapor pressure of the liquid and the pump suction pressure are known. The point to remember is that (neglecting velocity head and acceleration head) the amount of NPSH available to a pump is equal to the distance that the liquid would rise above the datum, from the suction line, before it starts to boil.
Figure 2. How to calculate NPSHA from pressure in a suction vessel (Acknowledgement is made to The Center for Professional Advancement, Applied Pump Technology Course)
Example Calculations of NPSHA
The following examples of NPSH calculations are provided by the Center for Professional Advancement from their course Applied Pump Technology, created by the late Igor Karassik.
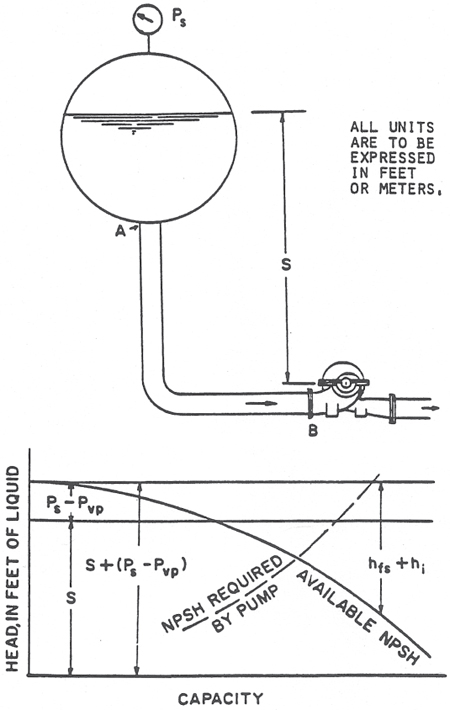NPSH = S + (Ps - Pvp) - (hfs + hi)
Where:
Pvp = Vapor pressure of lquid at pumping temperature
hfs = Friction losses in suction losses from A to B
hi = Entrance loss at A
NPSHA = ((Ps - Pv ) X 2.31)/SP. GRAVITY + Z - hf
Where:
Ps = Pressure over liquid surface, PSIA
Pv = Vapor pressure of liquid, PSIA
Z = Static head, FT
hf = Friction losses, FT
A) At Sea Level
NPSHA = ((14.7 - 0.5 ) X 2.31)/1.0 - 15 - 3 = 32.8 - 15 - 3 = 14.8 FT
B) At 5000-ft above sea level
NPSHA = ((12.2 - 0.5 ) X 2.31)/1.0 - 15 - 3 = 27 - 15 - 3 = 9.0 FT
Figure 3. Classical calculations of NPSHA. Note that using 0.5-psia as vapor pressure ignores effect of dissolved air. (Acknowledgement is made to The Center for Professional Advancement, Applied Pump Technology Course)
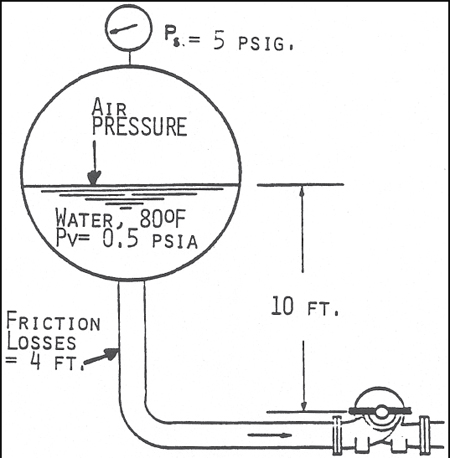
NPSHA = ((Ps - Pv ) X 2.31)/SP. GRAVITY + Z - hF
NPSHA = ((14.7 + 5 - 0.5 ) X 2.31)/1.0 + 10 -4 = 44.3 + 10 - 4 = 50.3 FT
NPSHA = ((Ps - Pv ) X 2.31)/SP. GRAVITY + Z - hF
Figure 4. Classical calculation of NPSHA with a Pressurized Suction Vessel. Note that using 0.5-psia as vapor pressure ignores effect of dissolved air. (Acknowledgement is made to the Center for Professional Advancement, Applied Pump Technology Course)
NPSHA = ((37.5 + 14.7 - 52.2 ) X 2.31)/0.56 + 10 - 2 = 0 + 10 - 2 = 8 FT
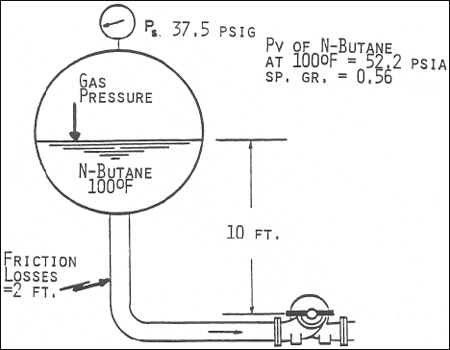
Figure 5. Calculation of NPSHA. Because the butane is at its bubble point, NPSHA requires no correction for dissolved gas. (Acknowledgement is made to The Center for Professional Advancement, Applied Pump Technology Course)
Note that the calculations illustrated in Figures 3 and 4 use 0.5-psia as the vapor pressure of the pumpage. This is a correct number for pure, deaerated water, but does not allow for any dissolved air. Because it has been exposed to air, the water in these examples contain a significant amount of dissolved air.
For Figure 3, if we follow the guideline of the Hydraulic Institute Standards (2), we must add 3-psi to the vapor pressure, which would reduce the NPSHA by 7-ft. If we follow Chen's (1) recommendation, we must add 6-to 7-psi (14- to 16-ft) to the vapor pressure. This would reduce the NPSHA to zero or less.
If we fail to account for the dissolved air, what will happen? We do not have a pump that sounds like it is pumping gravel, and we do not have an impeller chewed up by cavitation damage. Air does not do that. But the pump will exhibit a reduction in head, and may rumble a bit. A small amount of air injected into the inlet of a centrifugal pump will actually reduce cavitation noise and damage. (More on this in later months.)
References
1. Chen, C. C.,"Cope with Dissolved Gases in Pump Cavitation", Chemical Engineering, October, 1993
2. Hydraulic Institute Standards Hydraulic Institute, 9 Sylvan Way, Suite 360, Parsippany, NJ 07054‑3802
3. Whistler, A. M., "A Yardstick for NPSH Requirements", Petroleum Refiner, Jan., 1960
[[{"type":"media","view_mode":"media_large","fid":"377","attributes":{"class":"media-image","height":"50px","width":"100px"}}]]Pumps & Systems, April 2009