Determining pump speed using the affinity rules can be a challenge.
The days of inexpensive electricity are gone. With environmental pressures on the oil, coal and nuclear industries, electricity prices will likely rise. In today's economy, many companies explore options to reduce energy consumption to add to the bottom line or to simply stay in business. For companies that use centrifugal pumps, one method to reduce energy consumption is to install a variable speed drive to reduce the motor and pump speed. For some piping systems this is a great solution, but other solutions can be considered.It is important to understand how a pump and piping system interact and to understand the affect static head has on the pump's operating point. The pump affinity rules describe how a pump's performance will change with a change in pump speed, but the actual operating speed of the pump, and the energy savings, will depend on the amount of static and dynamic head in the system.
Systems with Differing Dynamic and Static Heads
Consider the three piping systems in Figure 1. Each system consists of a supply and product tank, a variable speed pump, valves and the interconnecting pipelines. The working fluid is water at 60 degrees F with a density of 62.37 pounds per cubic feet. Each system has the same pump selected to meet an operating point of 1,000 gallons per minute and 98 feet of total head at 1,735 rpm, but each has a different amount of static and dynamic head, achieved by varying the total pipe length and product tank elevations.
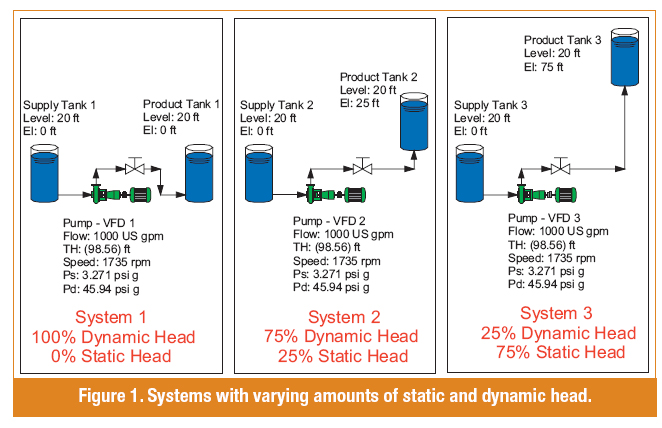
It is important to note that the pump does not know how much of its total head is allocated to static and dynamic head in the system. Static head is the sum of the difference in elevations of the liquid levels and surface pressures in both tanks. The dynamic head is the sum of the head losses in the pipelines, valves, fittings, and other components in the system. For pipelines, head loss can be calculated using the Darcy method shown in Equation 1, taken from the Crane Technical Paper No. 410 – Flow of Fluids Through Valves, Fittings, and Pipe.
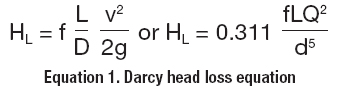
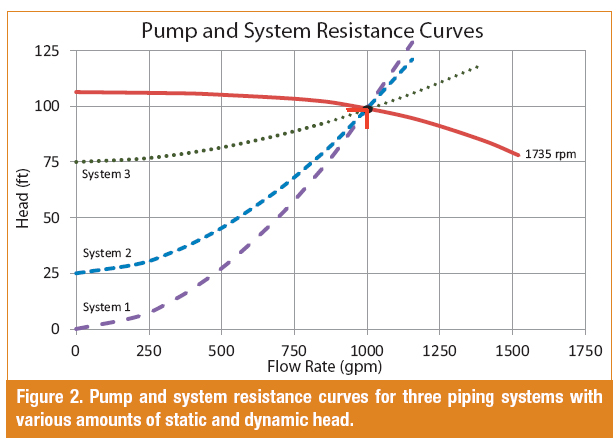
Although it appears that the head loss is a second order function of the flow rate, the Darcy friction factor (f) is also a function of the flow rate, which makes the head loss not quite a second order relationship. The pump and system resistance curves for these piping systems are shown in Figure 2.
System Static Head Affects Pump Speed in Variable Speed Applications
The pump affinity rules in Equation 2 describe how a centrifugal pump's flow rate (Q), Total Head (H), and power consumption (P) change with a change of impeller speed (N).
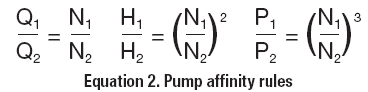
Since the flow rate changes in direct proportion to speed, and head changes proportional to the speed squared, a second order relationship exists between flow rate and head in pump performance as the speed changes. Mathematically, the affinity rules are easy calculations.
However, although the rules describe how the pump's performance will change with a change in speed, they do not show how a pump will perform with any particular piping system.
It is the piping system that determines what speed the pump has to run to overcome the static head and dynamic head at any given flow rate.
What is the pump speed needed to reduce the flow rate in each system in Figure 1 to 500 gallons per minute with the variable speed pump?
Using just the affinity rules, to reduce the flow rate by 50 percent the speed has to be reduced by 50 percent to 867.5 rpm:
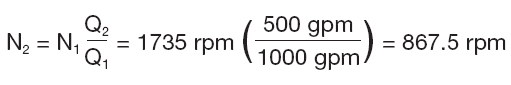
The affinity rules can then be used to determine the pump head at this speed:
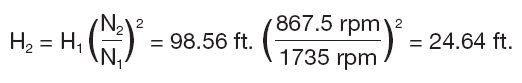
However, does the pump produce the amount of head required by the system at 500 gallons per minute? The total head needed by the system can be determined by calculating the pressures at the pump suction and discharge based on the Supply and Product Tank levels and pressures, the piping and valve losses, and the system flow rates. The required differential pressure across the pump can then be converted to head using Equation 3.
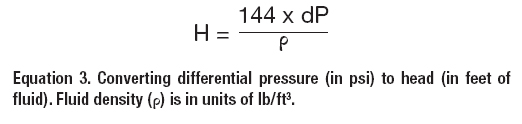

Figure 3 shows this for the three systems.
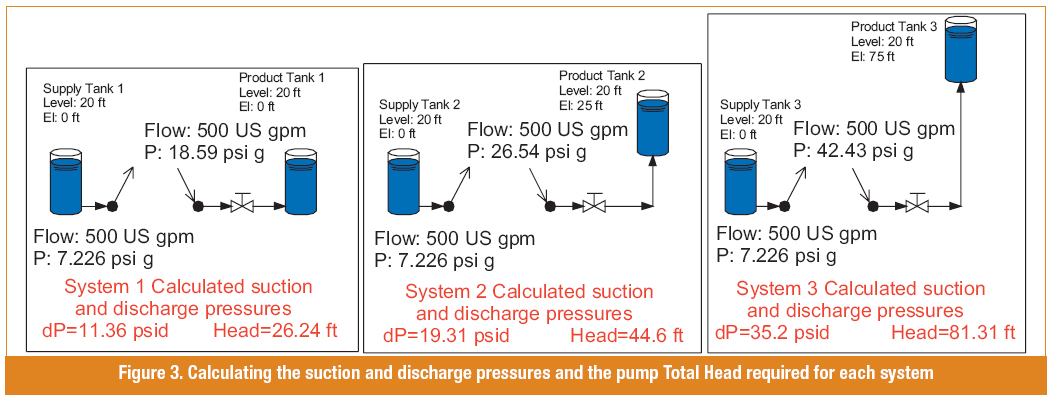
Figure 3. Calculating the suction and discharge pressures and the pump Total Head required for each system
Using Equation 3, the total head required by System 1 is:

The pump head calculated using the affinity rules was 24.64 feet, which is not enough to meet what the system requires at 500 gallons per minute, so the speed must be slightly higher to meet the needs of the system. Figure 4 shows the required pump speed needed to meet the head requirements of all three systems.
In order to meet the total head requirements of System 1 for a 50 percent flow reduction, the pump speed must be 895 rpm, compared to 867.5 rpm calculated using the affinity rule. This underestimation in pump speed is due to the fact that the system resistance is not quite a second order relationship to the flow rate.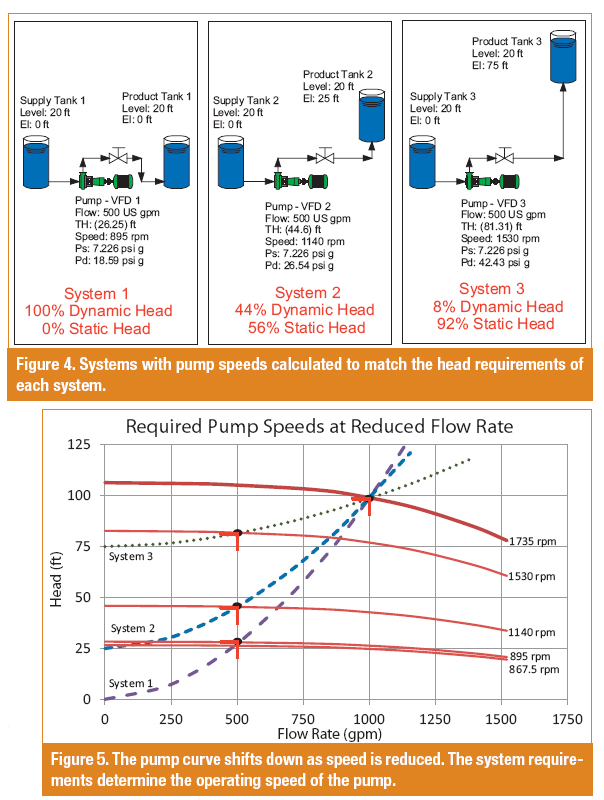
Underestimating the pump speed with the affinity rules is exacerbated by increasing the static head in the system. For Systems 2 and 3 in Figure 4, the total head requirements and the calculated pump speeds needed to meet them are even higher. Only the dynamic head is affected by a reduction in the flow rate. The static head stays the same as long as the difference between liquid levels and pressures between the two tanks stays the same.
The pump in System 2 requires a speed of 1,140 rpm to obtain a total head of 44.6 feet at 500 gallons per minute, whereas the pump in System 3 must run at 1,530 rpm because it requires 81.3 feet of total head. Using just the pump affinity rules in these cases would grossly underestimate the pump speed needed to reduce the flow to 500 gallons per minute. Figure 5 shows how the pump curve shifts down as the pump speed is reduced.
Effect of Static Head on Pump Efficiency and Energy Savings
The determination of pump speed for systems with static head also explains why the use of variable speed pumps in a system with a large amount of static head does not save as much money compared to a system with just dynamic head.
The affinity rules show that the power consumption is reduced by the cube of the change in pump speed, so the completely dynamic head system will consume much less power at the reduced flow rate because of the greater change in pump speed compared to the high static head system.
For the same 50 percent reduction in flow rate, System 1 saw a reduction in pump speed from 1,735 rpm to 895 rpm (840 rpm change). System 2 went from 1,735 rpm to 1,140 rpm (a 595 rpm change). System 3 went from 1,735 rpm to 1,530 rpm (205 rpm change).
The pump efficiency at the operating point is also affected by the static head. Figure 6 shows the pump and system resistance curves, as well as the ISO-efficiency lines to show how pump efficiency changes with a change in pump speed.
Figure 6 also shows the operating points for each system at the original and reduced flow rate. At 1,000 gallons per minute, all three pumps operate at about 88.6 percent efficiency.
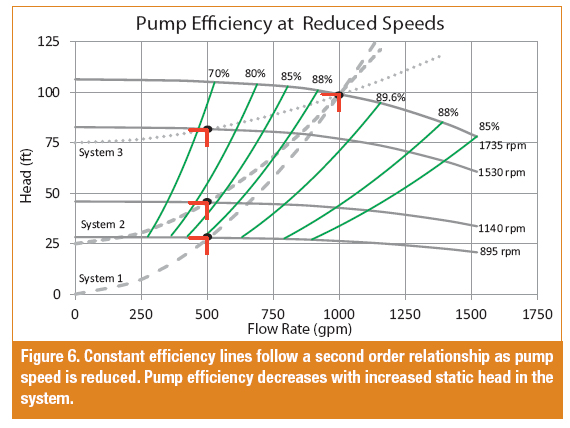
When the flow rate is reduced, the pumps in Systems 1, 2, and 3 operate at an efficiency of 88.3 percent, 83.1 percent and 72.4 percent, respectively.
To put all of this into perspective, assume each system is operated for half the year at 1,000 gallons per minute and half the year at 500 gallons per minute with an energy cost of $0.10 per kilowatt hour and motor efficiency of 93 percent.
Table 1 summarizes the energy costs and annual savings for each system as compared to operating the systems with a fixed speed pump at 1,750 rpm and using a throttle valve to control the flow rate.
Table 1. Operating costs and energy savings for systems with various amounts of static head
Conclusion
Static head in a system reduces energy savings when using a variable speed pump.
The pump affinity rules describe how the pump performance will change with a change in pump speed, but the actual operating speed of the pump will depend on the head requirements of the system.
The more static head the system has, the higher the pump speed needed to overcome this head.
In addition, the pump will operate farther back on its pump curve, resulting in lower pump efficiency at reduced flow rates.
The net effect of higher operating speeds and lower pump efficiency in systems with static head is a reduction in the energy savings when using variable speed pumps.
Pumps & Systems, June 2011

